What are Time Series Discords?
Learn how to use Matrix Profile Discords for anomaly detection.
What are Time Series Discords?¶
Time series discords have become one of the most effective and competitive methods in anomaly detection. First proposed by Keogh et al. [1], time series discords refer to the most unusual time series subsequences: those which are maximally different from all other subsequences in the same time series. The primary use of time series discords is to detect anomalies in a long time series.
Time Series Discord and K-th Time series Discord¶
Since the time series discord and the k-th time series discord have different definitions, it is necessary to keep these two concepts distinct.
In a narrow sense, a time series discord is a subsequence that is most dissimilar to its nearest neighbor, also known as the most significant discord (defined in [2]). We can easily spot the most significant discord from a Matrix Profile: the higher the Matrix Profile value, the greater the dissimilarity between the corresponding subsequence and its nearest neighbor, so the maximum value within a Matrix Profile indicates the time series discord (or the most significant discord).
The definition of time series discord also leads us to the discussion of the k-th time series discord. If we utilize a distance measure to quantify the dissimilarity between a time series subsequence and its nearest neighbor, the k-th time series discord is a time series subsequence with the k-th furthest distance from its nearest neighbor. You can imagine that to find the k-th discord, you first need to calculate distances between all subsequences and their nearest neighbors, then sort these distances from large to small, and finally select the subsequences with the k-th largest distance. This blog post provides you with a good intuitive example of top-k discord. In the next section, we will also illustrate the concept of the k-th discord with more specific examples.
For more information on Matrix Profile, please refer to this blog post.
How to Find Time Series Discords Using MPA?¶
In this section, we will demonstrate how to use the Matrix Profile API to mine time series discords and detect multi-scale anomalies in our sample dataset.
Dataset Overview¶
The sample dataset for this tutorial is taken and modified from the Italian power demand dataset in [3], representing the hourly electrical power demand in an Italian city for a total of 42 days (1,008 hours) from 02-23-1997 to 04-05-1997. This is a very interesting dataset, because it contains both a synthetic anomaly, as well as a natural change from winter regime to summer regime at the end.
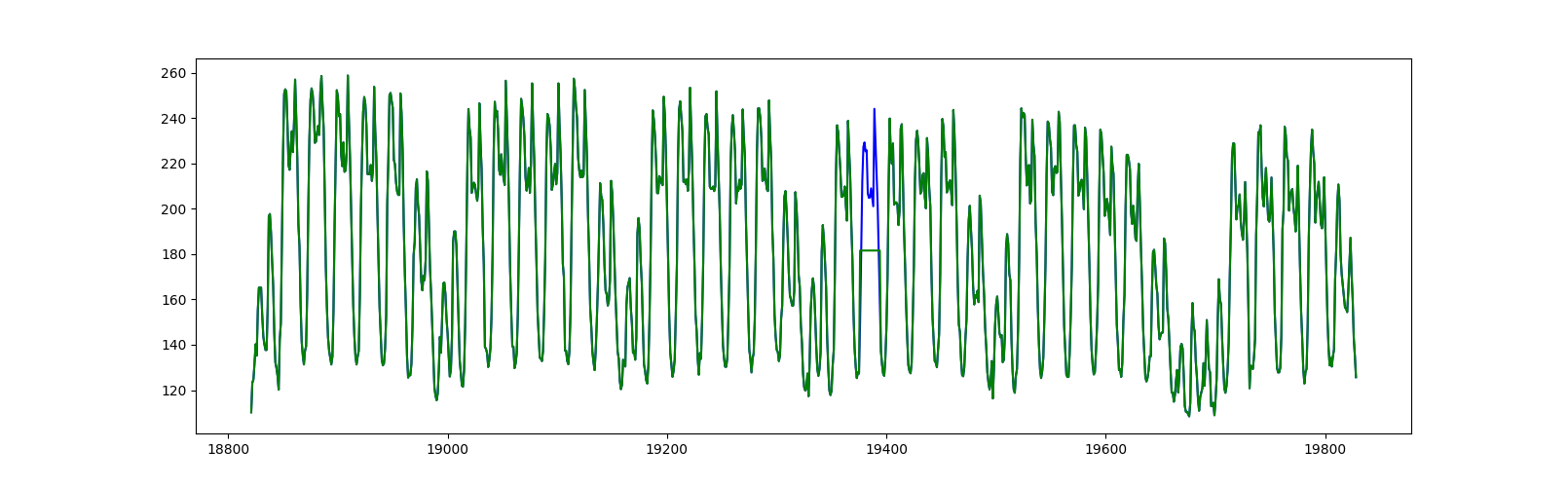
The figure above shows how we created a visually obvious anomaly. The blue represents the original data, and the green represents the data after an anomaly was introduced. Between 03-18-1997 and 03-19-1997, an anomaly is created by replacing a small fraction of original data (spaning 19 hours) with a constant region.
It's obvious that there are other anomalies in the sample dataset in addition to the synthetic anomaly. We will cover these in more detail in the Visualize Data section.
Analyze Sample Dataset with MPA¶
We'll start by finding out the synthetic anomaly using the Matrix Profile API.
Import Library and Load Data¶
import matrixprofile as mp
import numpy as np
from matplotlib import pyplot as plt
import pandas as pd
import matplotlib.ticker as ticker
# ignore matplotlib warnings
import warnings
warnings.filterwarnings("ignore")
# Load Data
input_file = 'AEM_data.txt'
f = open(input_file, 'r')
lines = f.readlines()
dataset = []
for line in lines:
dataset.append(float(line))
dataset = np.array(dataset)
Visualize Data¶
Here we visualize our sample data with a timestamp so that we can easily see where anomalies locate.
dates = pd.date_range(start = '19970223', end='19970406', freq = 'h').strftime("%Y-%m-%d %H:%M:%S").to_list()
plt.figure(figsize=(20,6))
plt.plot(dates,dataset,'g')
plt.title('Power Demand in Italy')
plt.ylabel('Power Supply from HV Grid (MW)')
plt.xlabel('Datetime')
plt.xticks(rotation=90)
plt.gca().xaxis.set_major_locator(ticker.MultipleLocator(24))
plt.show()
It's not hard to see that the sample dataset is a periodic dataset with repeated patterns. One cycle is about 7 days (that is, one week), beginning on Sunday. 1997-02-23, 1997-03-02, 1997-03-09, 1997-03-16, 1997-03-23 and 1997-03-30 are all Sundays.
What's more, except for the 19-hour synthetic anomaly introduced on 1997-03-18, there are two other anomalies of different lengths in this dataset. If looking closely at the power supply data for 1997-03-30 (Sunday) and 1997-03-31 (Monday), we will find that they are much less than the normal power supply data on other Sundays and Mondays, which suggests a potential anomaly. Also, after 1997-03-30, the patterns of data are not the same as before, which implies a regime change (also an anomaly in this example).
In the following sections, we will demonstrate how to leverage MPA to discover all these different anomalies.
Compute Matrix Profile, Discover Discords and Visualize¶
Since the dataset is at one-hour intervals and we know beforehand that the length of the synthetic anomaly is 19 hours, the window_size is set to 19 to compute the Matrix Profile and discover discords of length 19. Here we set k to 1 to highlight the most significant discord. The parameter exclusion_zone is assigned to 19 to avoid trivial matches. You may refer to this blog post to learn more about the setting of exclusion_zone.
Please note that it does not necessarily require a priori knowledge of anomaly length to set the window size. We can also try to run the code multiple times with different window sizes until finding the optimal one. For example, If we are interested in anomalies that occur within one day, we can try each window_size in order within 24. In this example, to better see the most significant discord and its corresponding Matrix Profile, we set the parameter window_size to the exact length of the anomaly.
window_size = 19
k = 1
profile = mp.compute(dataset, window_size)
profile = mp.discover.discords(profile, k = k, exclusion_zone = window_size)
mp.visualize(profile)
plt.show()
mp_adjusted = np.append(profile['mp'], np.zeros(profile['w'] - 1) + np.nan)
fig, ax = plt.subplots(1, 1, sharex=True, figsize=(16,4))
ax.plot(np.arange(len(profile['data']['ts'])), profile['data']['ts'])
ax.set_title('Window Size {}'.format(str(window_size)))
ax.set_ylabel('Data')
flag = 1
for discord in profile['discords']:
x = np.arange(discord, discord + profile['w'])
y = profile['data']['ts'][discord:discord + profile['w']]
if flag:
ax.plot(x, y, c='r',label="Discord")
flag = 0
else:
ax.plot(x, y, c='r')
plt.legend()
plt.show()
As can be seen from the figures above, the MPA pinpoints the location of the synthetic anomaly in the sample dataset. Since there's no continuous 19-hour constant region in the power supply data on any other day, the Matrix Profile value corresponding to the synthetic anomaly is the largest when the window size is 19. Therefore, the time series subsequence consisting of constant values is recognized as the most significant discord (it can be seen in the second-to-last figure) and marked in red in the last figure.
Discover Time Series Discords in Different Scales¶
As mentioned in the previous section, the sample dataset contains multiple anomalies, and these anomalies are multi-scale. In addition to the 19-hour synthetic anomalies, there are also anomalies that span two days and approximately one week in the sample dataset.
The Matrix Profile API can still help us deal with multi-scale anomalies in the dataset, just by adjusting the window_size and k parameters.
Unusual Sunday and Monday¶
Because we are now concerned about whether there are 2-day anomalies in the sample dataset, we adjusted the window_size to 48. At the same time, the k is set to 2 to display the top two discords. Unlike the previous example, we only plot the discords this time.
from matrixprofile.visualize import plot_discords_mp
window_size = 2*24
k = 2
profile = mp.compute(dataset, window_size)
profile = mp.discover.discords(profile, k = k, exclusion_zone = window_size)
plot_discords_mp(profile)
plt.show()
discord_num = list(range(1,k+1))
for i in range(len(discord_num)):
if i == 0:
discord_num[i] = str(discord_num[i])+"st"; continue
if i == 1:
discord_num[i] = str(discord_num[i])+"nd"; continue
if i == 2:
discord_num[i] = str(discord_num[i])+"rd"; continue
discord_num[i] = str(discord_num[i])+"th"
mp_adjusted = np.append(profile['mp'], np.zeros(profile['w'] - 1) + np.nan)
fig, ax = plt.subplots(1, 1, sharex=True, figsize=(16,3))
ax.plot(np.arange(len(profile['data']['ts'])), profile['data']['ts'])
ax.set_title('Window Size {}'.format(str(window_size)))
ax.set_ylabel('Data')
for i,discord in enumerate(profile['discords']):
x = np.arange(discord, discord + profile['w'])
y = profile['data']['ts'][discord:discord + profile['w']]
ax.plot(x, y, c='C'+str(i+3),label="{} Discord".format(discord_num[i]))
plt.legend()
plt.show()
As you can see from the figures above, the MPA locates the position of the anomaly that occurs on 1997-03-30 (Sunday) and 1997-03-31 (Monday) and marks it in red in the last figure. Since the power supply data of these two days is much smaller than that of other Sundays and Mondays, its Matrix Profile value is the largest when the window size is 48. Therefore, the time series subsequence corresponding to the unusual Sunday and Monday is recognized as the most significant discord, which can be seen in the last two figures.
In particular, if we set k to greater than 1, the MPA will find other unusual subsequences, namely k-th discord, in addition to the most significant discord. In our case, the second discord discovered by MPA (and marked in purple) also contains the synthetic anomaly that we discussed in the previous section, which makes perfect sense. Because the two-day data with a constant region is visually dissimilar to other data that spans two days, it can also be regarded as one of the anomalies in the dataset.
Regime Change¶
In this example, the Matrix Profile API can also be used to detect the change from the winter regime to the summer regime. (The shorter summer regime is considered as an anomaly in our example)
Although we don't know the exact location of the regime change and the length of the anomaly, we can estimate the window_size with some reasonable values. As we know, the period of the sample dataset is about one week, so we adjust the window_size to 7 × 24, which is 168 hours. The k is unchanged at 2. Let's see what happens after we make this adjustment.
window_size = 7*24
k = 2
profile = mp.compute(dataset, window_size)
profile = mp.discover.discords(profile, k = k, exclusion_zone = window_size)
plot_discords_mp(profile)
plt.show()
discord_num = list(range(1,k+1))
for i in range(len(discord_num)):
if i == 0:
discord_num[i] = str(discord_num[i])+"st"; continue
if i == 1:
discord_num[i] = str(discord_num[i])+"nd"; continue
if i == 2:
discord_num[i] = str(discord_num[i])+"rd"; continue
discord_num[i] = str(discord_num[i])+"th"
mp_adjusted = np.append(profile['mp'], np.zeros(profile['w'] - 1) + np.nan)
fig, ax = plt.subplots(1, 1, sharex=True, figsize=(16,3))
ax.plot(np.arange(len(profile['data']['ts'])), profile['data']['ts'])
ax.set_title('Window Size {}'.format(str(window_size)))
ax.set_ylabel('Data')
for i,discord in enumerate(profile['discords']):
x = np.arange(discord, discord + profile['w'])
y = profile['data']['ts'][discord:discord + profile['w']]
ax.plot(x, y, c='C'+str(i+3),label="{} Discord".format(discord_num[i]))
plt.legend()
plt.show()
From the figures above, we can see that the MPA roughly identifies the location of the summer regime (an anomaly in our case). Because of the great difference in pattern between the summer regime and the winter regime, when windows size is 7 * 24, the Matrix Profile value corresponding to the shorter summer regime is the largest. Therefore, the time series subsequence of the summer regime is recognized as the most significant discord and marked in red in the last figure.
Similarly, the second discord marked in purple also contains the anomaly we synthesized because the time series subsequence with a constant region looks different from any other 7-day subsequence.
Reference¶
[1] Keogh, E., Lin, J., & Fu, A. (2004). HOT SAX: Finding the most unusual time series subsequence: Algorithms and applications. In Proc. of the 5th IEEE Int'l Conf. on Data Mining (pp. 440-449).
[2] Yankov, D., Keogh, E., & Rebbapragada, U. (2008). Disk aware discord discovery: finding unusual time series in terabyte sized datasets. Knowledge and Information Systems, 17(2), 241-262.
[3] Imani, S., Madrid, F., Ding, W., Crouter, S., & Keogh, E. (2018, November). Matrix Profile XIII: Time Series Snippets: A New Primitive for Time Series Data Mining. In 2018 IEEE International Conference on Big Knowledge (ICBK) (pp. 382-389). IEEE.

Comments
Comments powered by Disqus